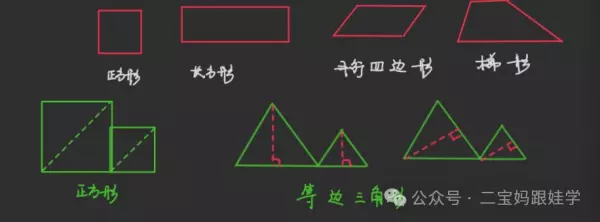
一、基本图形的面积公式
1、正方形面积=边长×边长
2、长方形面积=长×宽
3、平行四边形面积=底×高
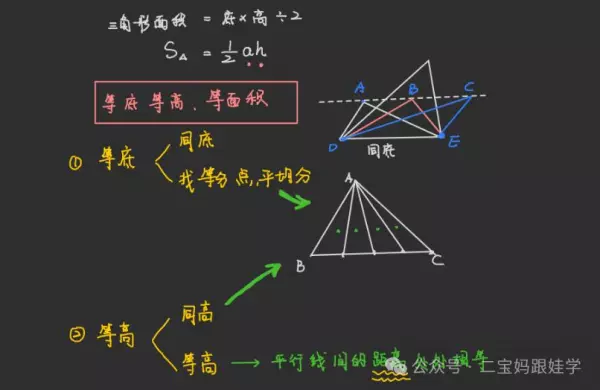
4、三角形面积=底×高÷2
5、梯形面积=(上底+下底)× 高÷2
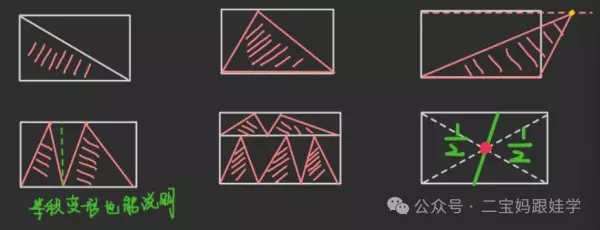
二、等积变形
1、定义:图形的形状发生改变,但面积保持不变。
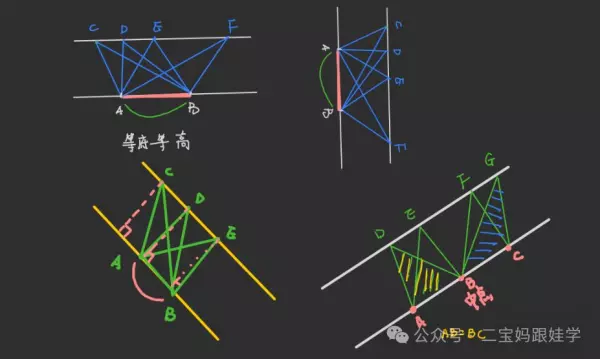
2、本质:等底等高(平行线间的距离处处相等)
3、关键:
找到平行线间“顶天立地”的三角形,固定底边,移动顶点,也叫拉窗帘。
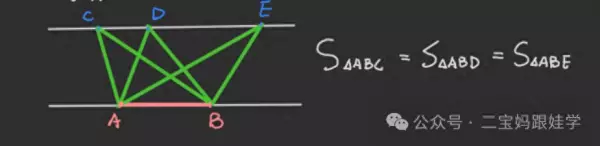
4、常见的平行线
1)长、正、平的对边,梯形的上底和下底。
2)组合图形
5、类型
(1)整体变形
(2)局部变形
(3)多次变形(滚雪球)
三、探索
1、如果一条直线把一个平面图形的面积分成相等的两部分,我们把这条直线称之为这个图形的一条面积等分线。请你画出几条三角形的面积等分线.
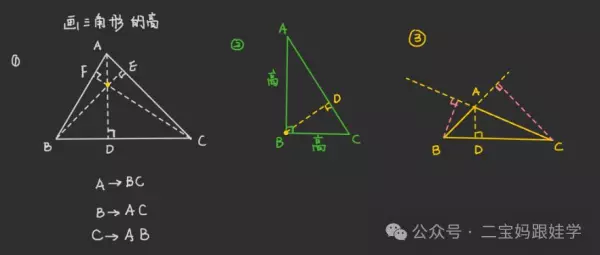
2、拓展,画三角形的高
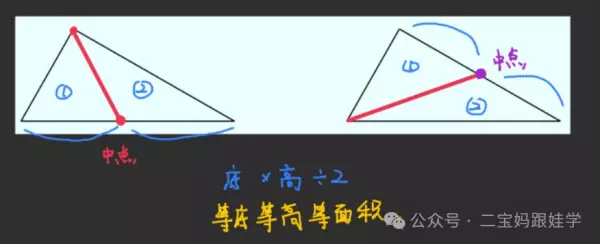
3、三角形的面积,等底等高等面积。
4、画平行线找三角形的高
四、一半模型
1、长方形(平形四边形)中的一半模型。如下图:
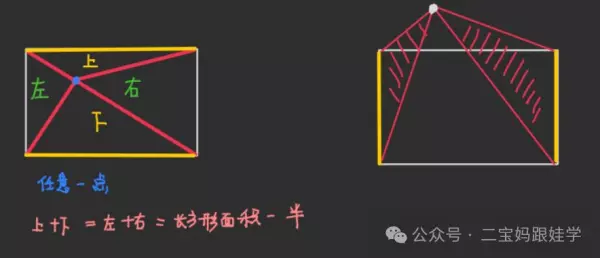

3、任意四边形
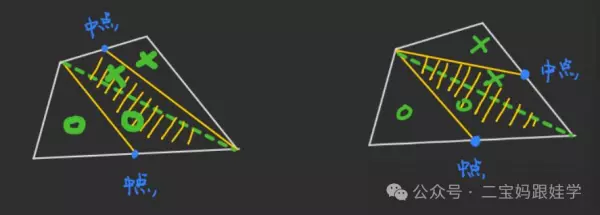
五、经典例题
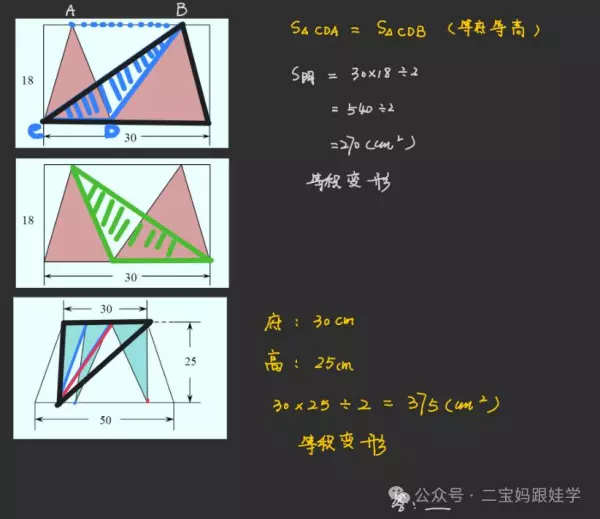
1、请分别计算长方形和梯形中阴影部分的面积。(单位:厘米)
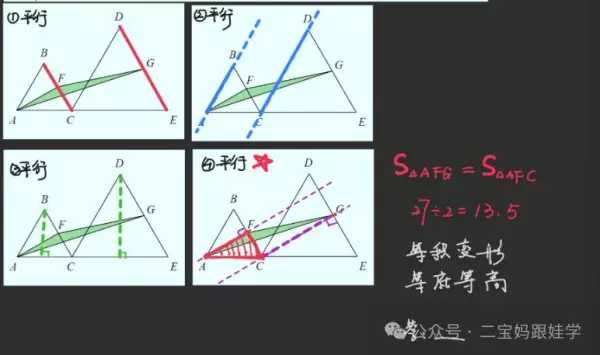
2、如图,点C在线段AE上,三角形ABC和三角形CDE都是等边三角形,且F是线段BC的中点,G是线段DE的中点,若三角形ABC的面积为27,三角形AFG(阴影部分)的面积是多少?
3、如图中三个正方形的边长从左到右依次减半,最小正方形的边长为3,那么图中阴影部分的面积是多少?
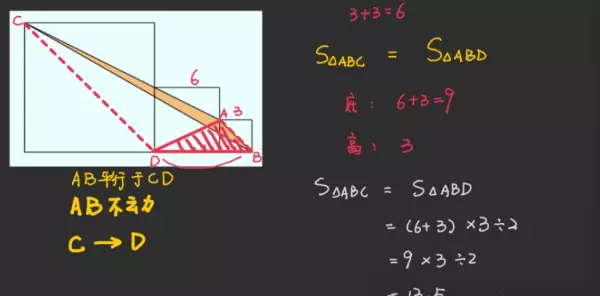
4、三个正方形ABCD、BEFG、CHI如图所示摆放,已知正方形ABCD的边长为10,正方形BEFG的边长为6,阴影部分的面积是多少?
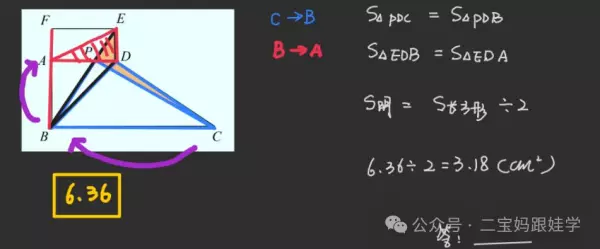
5、四边形ABCD是个直角梯形(∠DAB=∠ABC=90°),以AD为一边向外作长方形ADEF,其面积为6.36平方厘米,如图所示,连接BE交AD于P,再连接PC.则图中阴影部分的面积是多少?
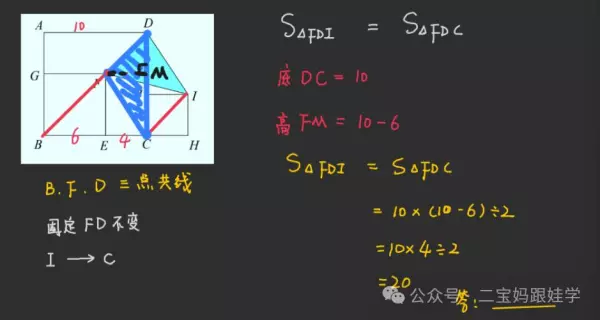
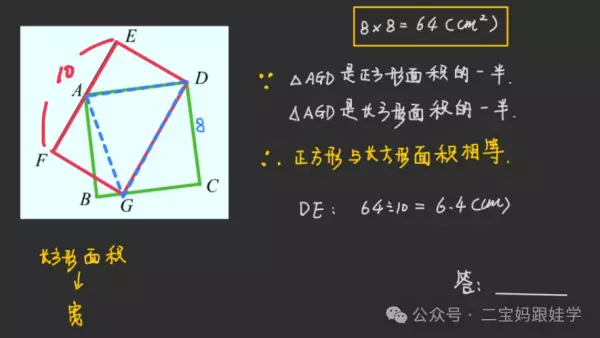
6、如图,有一个长方形和一个正方形重叠在一起,如果正方形ABCD的边长是8厘米,长方形DEFG的长DG=10厘米,那么宽DE长多少厘米?
解析,如下图所示:
7、如图所示,平行四边形ABCD中AB和EF平行,三角形ABF的面积是20平方分米,三角形ECD的面积是24平方分米,求平行四边形ABCD的面积。
解析,如下图所示:

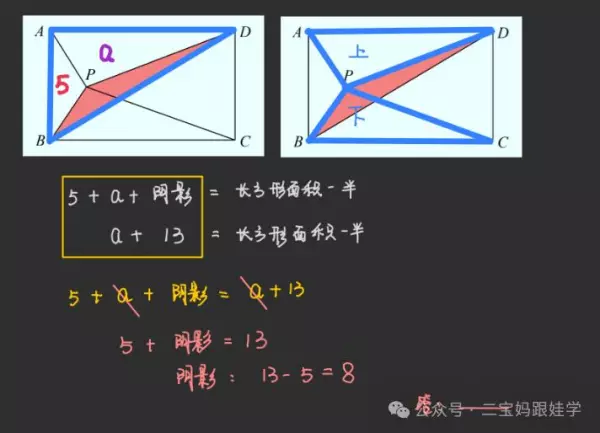
8、P是长方形ABCD内一点,三角形PAB的面积等于5,三角形PBC的面积等于13。问三角形PBD的面积是多少?
解析,如下图所示:
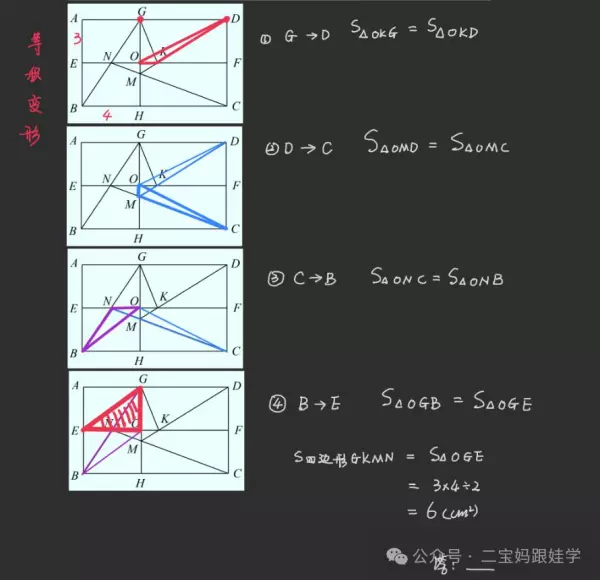
9、在长方形ABCD中,点E、G分别在AB、AD上,且AE=3cm,BH=4cm,EF//AD,GH//AB,连接BG交EF于点N,连接CN交GH于点M,连接DM交EF于点K,连接GK,如下图所示,求四边形GNMK的面积。