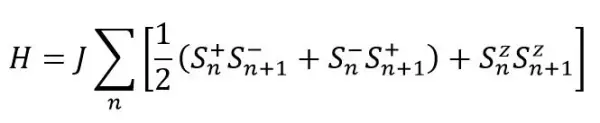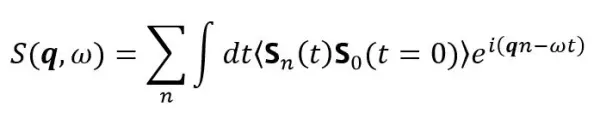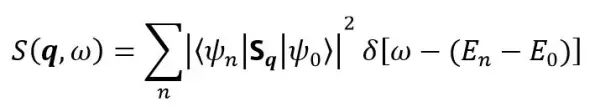1.引子
成语“泾渭分明”,出自《诗经•邶风•谷风》:“泾以渭浊,湜湜其沚”。成语描述了泾河水浊、渭河水清,但泾河的水流入渭河时,清浊不混,比喻界限清楚或是非分明。
在详解高、低能磁激发有何不同之前,有必要先铺垫一些基础内容,以便于读者更清晰明了我们的主题是什么、我们的研究目的和意义在哪里。
2.磁激发——磁性材料自旋动力学
固体材料由大量粒子(如电子、离子)所组成。当这些粒子之间存在很强的相互作用时,体系就构成一个复杂的量子多体系统,呈现出丰富的物质相与相变。如果电子库仑相互作用比较强,体系将会变成一种莫特绝缘体。此时,电子失去巡游性,局域在离子实周围轨道上,而且相邻离子实周围的电子自旋或轨道磁矩之间具有关联相互作用。这一图像表明这是一个磁性强关联系统,表现出宏观的磁性或非磁基态。
目前,实验探测材料属性的手段,都基于对系统施加某种刺激扰动(光、电、中子等轰击材料),系统对刺激产生响应。我们则根据输入、输出信号,并结合能量、动量守恒等物理规律,去反推出材料的本征性质。举个例子,我们往池塘里和充满沥青的大缸里分别扔一块石头:沥青明显难以漾起大的波澜,而水塘则可能是波澜壮阔。根据波澜的程度,我们就知道水和沥青的粘度是不一样的。凝聚态物理研究中,这样的石头很多,其中之一类即非弹性中子散射:借助带磁矩的中子去轰击材料、施加扰动,然后根据实验散射谱,来回看磁性系统的磁激发行为。物理研究,莫不是如此逻辑,屡试不爽。
当然,实验得到这个磁激发谱只是第一步,如何理解这个磁激发谱背后蕴含的磁性系统本征性质,就需要理论物理学者的支持。理论计算上,强相互作用的量子多体系统非常复杂,严格求解它们并不容易。举个简单的例子:后文我们将要计算的一维模型有192个相互作用的自旋,每个= 1/2自旋代表着两个自由度(具有两个局域自由度)。如果严格求解这个体系的定态薛定谔方程的全部能谱和波函数,就需要对一个2维度的矩阵做对角化。如此,就算把全世界的超级计算机都用上,都求解不了。
借助这些适用于量子多体系统的数值方法,物理人可以对材料的磁激发谱进行理论模拟复现,以研究各种激发模式的谱学特征。通过与实验结果的比对和交叉求证,我们得以对材料的本征物理性质有更深入理解。果若如此,乃为美妙之事。
磁激发谱的研究,除了满足物理人对物理问题的好奇心和科学知识探索外,它总要有点用处。当然,磁激发谱的实际应用价值也很大,包括不同层面的应用预期。例如,可以利用磁有序系统的磁激发准粒子(如自旋波等),来做低功耗的自旋电子学器件。非磁基态如量子自旋液体等,还可以表现出“自旋子”(spinon)等分数磁激发现象。这种自旋子因抗干扰能力强、相干长度好等,未来可以成为拓扑量子计算和量子存储的理想载体。综合两者,磁激发研究,一直是当前凝聚态物理中一个重要的前沿科学问题。
3.海森堡模型——研究磁性的基本物理模型
1981年,法捷耶夫和塔赫塔江,利用贝特拟设揭示了一维自旋= 1/2反铁磁海森堡链的元激发为自旋子[2]。1983年,诺贝尔奖得主霍尔丹发现了整数自旋链和半整数自旋链之间的主要区别[3]。这些成果使得人们对新型准一维磁性材料的兴趣高涨,从而大大推进了相应的理论和实验技术的发展。
后来,高温超导与中子散射为低维材料的研究带来了新的活力。一维自旋= 1/2的海森堡模型,是描述低维量子磁性的重要范例。比如,在加横场的准一维反铁磁材料BaCoVO中观察到了E8粒子[4]。各向同性的海森堡模型的哈密顿量为:
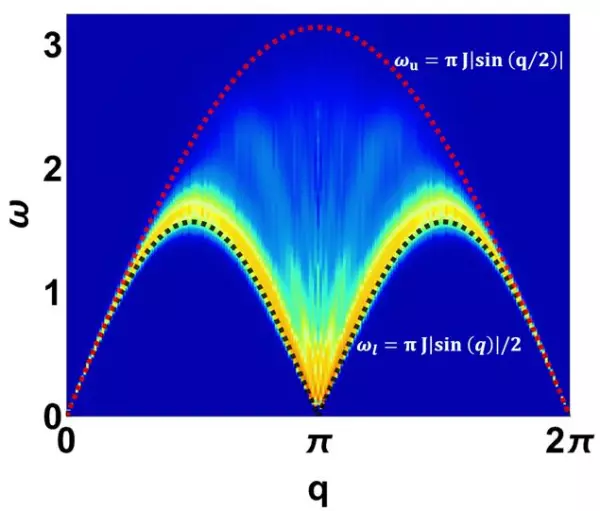
其中为相互作用强度,系统满足SU(2)和平移对称性。通过贝特拟设,可得到其元激发为无能隙的双自旋子连续谱[2]。图1展示了量子蒙特卡罗的模拟结果,分别有下界ω= π · J |sin| / 2和上界ω= π · J |sin|。这里的双自旋子连续谱,来源于反铁磁基态中的一个自旋翻转,形成|ΔM| = 1的激发。由于一维系统不受链间相互作用的影响,|ΔM| = 1的激发分裂成两个畴壁,即两个自旋子。每一个自旋子,携带自旋为1 / 2,可在链上自由移动[5]。
自旋子的运动,是研究拉廷格液体理论预言的自旋-电荷分离现象的重要基础[6]。后文的图7(a)展示了两个自旋子的形成过程。这两个自旋子犹如一对脱离父母手心的双胞胎,在一条狭窄的小路上沿着两个方向自由奔跑。
图1.量子蒙特卡罗模拟的双自旋子连续谱。
4.动力学结构因子——沟通非弹性中子散射实验的桥梁
自旋动力学结构因子包含了系统涨落的空间和时间关联信息,是连接磁激发的理论与实验研究非常重要的纽带。它的定义可以表达为:
其中是波矢,ω是频率。通常在理论计算中,我们都是设普朗克常数ℏ = 1,所以有E = ℏω = ω,这里的ω反映的是能量的大小。这一动力学结构因子,是对自旋关联函数做了双重傅里叶变换(实空间→动量空间,时间→能量)得到的。由此,它还可以有另一种定义:
其中|ψ代表第个本征态,对应的本征值为;|ψ即为基态,相应的能量为。是指动量空间中的自旋算符。
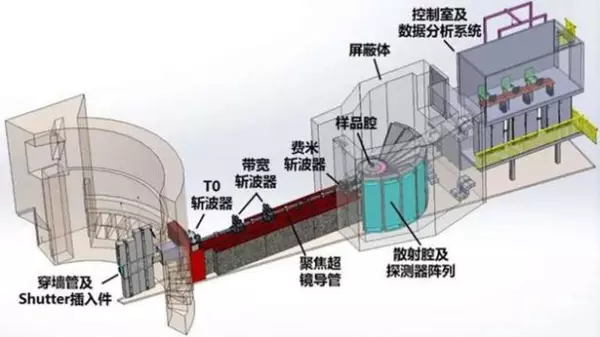
动力学结构因子的理论计算结果,可直接与非弹性中子散射、共振非弹性X光散射实验的结果进行对比,因此受到理论和实验物理人的双重青睐。值得一提的是,中山大学建设的高能直接几何非弹性中子散射飞行时间谱仪(简称“中大谱仪”),是中国首个高能非弹性中子散射谱仪,也是中国首台具有中高能磁激发谱和声子谱探测能力的材料动力学性质研究谱仪[7]。中大谱仪预计今年投入使用,实验和理论物理人都已经迫不及待地等候这个科研装置启动的那一天,期待能够在中高能磁激发等研究上有新的研究发现。
图2.中大谱仪结构示意图[6]。
5.中高能磁激发——丰富多彩的准粒子
磁激发体现物质的自旋动力学,对理解高温超导机理、探索自旋之间的量子纠缠,指导研发磁电子器件起着重要的作用。传统的观念认为,一个磁有序系统的磁激发,主要是自旋波(Magnon)。但是,对一些具有团簇结构量子自旋系统的高能激发谱,自旋波描述总是缺乏可信度,相应的高能准粒子激发机制始终不清晰。
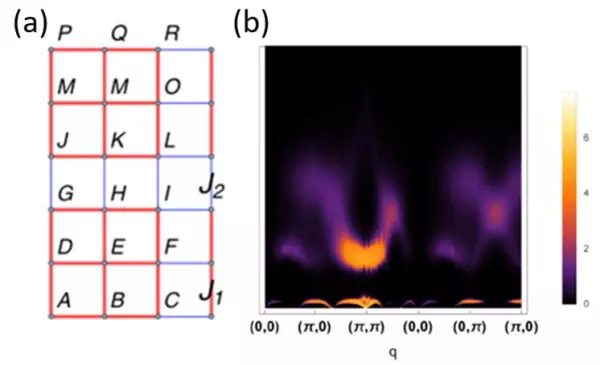
图3. 3x3棋盘结构自旋模型的示意图,(b) = / = 0.1时的磁激发谱[9]。
相比于低能激发,量子磁体的高能激发研究还比较缺乏。高能激发并不是简单的自旋波,有时会出现反常的激发特征,因此吸引了越来越多物理人的兴趣。例如,在高温超导反铁磁材料LaCuO中,非弹性中子散射观察到的高能激发就出现了反常:高能自旋波在倒易空间处分数化为自旋子[8]。2019年,姚道新教授团队研究了不同棋盘结构的二维模型自旋激发谱[9],如图3所示。其中的3x3结构(也叫田字格)激发谱是无能隙的,在低能处形成具有周期结构的连续谱。这是因为,每个团簇包含奇数个自旋,可重整化为单一自旋= 1/2,高能谱与低能谱之间有明显的能隙。而高能部分,不再是自旋波激发,具体的准粒子是什么,目前还没有定论。
为了探讨高能激发机制,我们不妨将上述二维模型简化为一维的三聚体反铁磁自旋链,以此来寻找高能激发中的物理规律。
图4.一维反铁磁三聚体自旋链系统的示意图[12]。
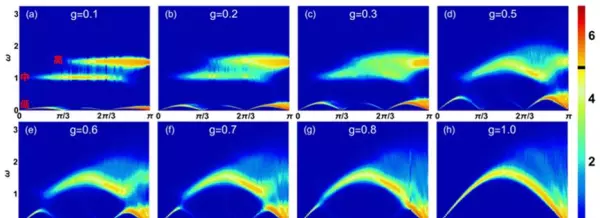
图5.通过量子蒙特卡洛方法得到的动量空间磁激发能谱[12]。
6.反铁磁三聚体自旋链——分数化组合型激发
我们利用量子蒙特卡洛、精确对角化和微扰理论解析,系统研究了反铁磁三聚体自旋链(见图4)的磁激发特性。
(1)通过改变三聚体间耦合强度和三聚体内耦合强度的比率=/,我们展示出系统具有非常丰富的磁激发谱(见图五)。
(2)在三聚体简并基态形成的有效希尔伯特空间中,可以获得描述低能部分的有效模型,乃= 1/2的海森堡自旋链。因此,当= 1时,宽度为~的双自旋子连续谱演变为g → 0时宽度为~的类似连续谱。
(3)由于较弱的三聚体间相互作用,系统激发是局域化在三聚体内的激发,中能和高能模不能用自旋波或者自旋子来描述。根据相应的激发机制,中能和高能准粒子分别被称为双重子(Doublon)和四重子(Quarton)。这里的“重”读chóng、第二声,代表简并,并不是粒子物理中的重zhòng子、读第四声。这些新奇的高能磁激发超越了传统的重整化描述。
图6.泾河与渭河交汇[10]。
现在,回到我们的主题:泾渭分明的高、低能磁激发。
当= 0.1时,如图5(a)所示,低能激发呈现周期性的结构,对应于一条具有均匀相互作用的有效反铁磁海森堡链。所以,低能准粒子依旧是自旋子,携带自旋1/2。这里的低能激发,因为只包含有自旋子,相应的激发机制一清二楚,犹如渭河一般清澈见底(如图6所示)。
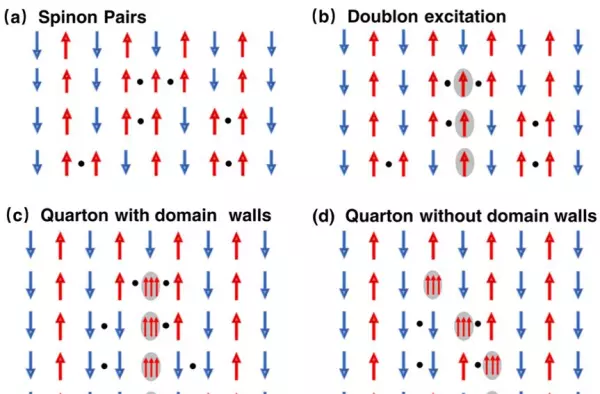
中、高能两条近似的平带,来源于三聚体内部的激发,对应的准粒子已经不再是常见的磁振子。根据激发机制,中能和高能的准粒子分别被命名为“双重子”和“四重子”,各自携带自旋= 1。图7展示了自旋子、双重子和四重子的实空间示意图。
所谓自旋子,携带自旋1/2,是翻转一个自旋形成的。它们通常成对出现,在一维自旋链上自由移动。双重子和四重子的示意图中,箭头代表三聚体的有效自旋。有效自旋的翻转,意味着三聚体内能级的跃迁。如图7(b)所示,中间蓝色的有效自旋向上翻转,代表被激发的三聚体由基态跃迁到第一激发态,产生|ΔM| = 1的激发。被翻转的有效自旋与周围的有效自旋形成两个畴壁,即两个自旋子。
激发的三聚体,对这两个自旋子有一定的束缚作用,不再是图7(a)中所示的自由自旋子。最终形成被激发的三聚体周围,伴随着两个自旋子共同在自旋链上传播。双重子没有被分数化,故所携带的自旋为= 1。
类似地,高能激发也可以用三聚体内的能级跃迁来解释。区别在于四重子形成过程中存在两种情况:有自旋子伴随和无自旋子伴随(分别如图7(c)和(d)所示)。高能激发产生的四重子携带的自旋也是= 1。因此,中能的双重子和高能的四重子激发都是组合型的激发。
当= 0.2时,如图5(b)所示,中、高能首先融合形成新的高能谱。此时,高能谱包含双重子、四重子和自旋子,犹如泾河一样浑浊,让人琢磨不透。随着增大到0.7附近,如图5(f)所示,高、低能激发谱之间的能隙闭合,泾河的水流入渭河,高能部分的多种准粒子也开始分数化为自旋子。这种情况持续延续,直到= 1时,如图5(h)所示,系统演变为均匀的海森堡自旋链。此时,所有的高能准粒子都分数化为自旋子,两河之水最终都融为一体、不再有泾渭之分。
当然,我们期望此时的水还是清澈的,因为这样可以完美符合= 1时只有自旋子一种准粒子的描述。需要强调一点,这里引入泾渭分明只是为了说明高、低能激发的不同之处,并不是为了说明高、低能融合之后依旧界限分明。
图7.实空间中自旋子、双重子和四重子的示意图[12]。
在材料中,如果能够识别出具有线性三聚体结构且的准一维量子磁体,则在非弹性中子散射实验中应能观察到这些特征。目前,已经有一些近似三聚体耦合的量子磁体,例如ACu, A =。在PbCu(PO)的非弹性中子散射谱中,已经观察到有ω ~ 9 meV和ω ~ 13.5 meV两个平带的激发谱[11]。在理论结果中,当= 0.1时(见图5(a)),中能和高能激发也揭示了这一激发谱特征。这些结果能为探索高能分数化激发提供可靠的理论支持。
7.结语
量子磁性,是当前凝聚态物理中极其重要的科学前沿。它与新物态、高温超导、量子计算等都有密切的关联,在基础和应用上都有重要的价值。
在量子磁性系统中,量子涨落和相互作用之间的竞争,不仅会产生新奇的磁性基态,例如量子自旋液体、自旋玻璃、价健固体等,也会产生非同寻常的磁激发行为,例如分数激发、弦激发、多磁振子激发、拓扑激发等。这些物理现象及其深刻理解,在物理学和信息科学等领域有潜在的重要价值。
本项研究工作,在一个看似简单的物理模型中找到了不简单的高能激发机制。高能激发,犹如冰面下的世界,不破冰就很难发现其是否丰富多彩。破冰过程,类似探索之路,漫长而又艰辛。但是对于未知的渴望总是带来不灭的热情,驱动着研究者去发现新的大陆。
参考文献
[1]熊梓健、姚道新,“Beat阻挫磁性”,《量子材料》公众号,2021。
L. D. Faddeev and L. A. Takhtajan. Phys. Lett. A 85, 375 .
F. D. M. Haldane. Phys. Lett. A 93, 464 – 468 .
H. Zou, Y. Cui, X. Wang, Z. Zhang, J. Yang, G. Xu, A. Okutani, M. Hagiwara, M. Matsuda, G. Wang, G. Mussardo, K. Hódsági, M. Kormos, Z. He, S. Kimura, R. Yu, W. Yu, J. Ma, and J. Wu, Phys. Rev. Lett. 127, 077201 .
H. -J. Mikeska and A. K. Kolezhuk. One-dimensional magnetism. In: U. Schollwöck, J. Richter, D. J. J. Farnell, R.F. Bishop Quantum Magnetism. Lecture Notes in Physics 645, 1 – 83 .
[6] F. He, Y. Z. Jiang, H. Q. Lin, R. G. Hulet, H. Pu, and X. W. Guan,Phys. Rev. Lett. 125, 190401 (2020)
N. S. Headings, S. M. Hayden, R.Coldea, and T. G. Perring, Phys. Rev. Lett. 105, 247001 .
Y. Xu, Z. Xiong, H. Q. Wu, and D. X. Yao, Phys. Rev. B 99, 085112 .
M. Matsuda, K. Kakurai, A. A. Belik, M. Azuma, M. Takano, and M. Fujita. Phys. Rev. B 71, 144411 .
J. Q. Cheng, J. Li, Z. Xiong, H. Q. Wu, A. W. Sandvik, and D. X. Yao. npj Quantum Mater. 7, 3 .
备注:
(2)这里推介的论文其他作者包括:李军,曾在姚道新教授课题组担任副研究员,现在燕山大学工作;熊梓健曾是姚道新教授课题组的博士研究生,现在重庆大学工作;邬汉青,任职中山大学物理学院副教授;A. W. Sandvik任职波士顿大学教授。
转载内容仅代表作者观点
不代表中科院物理所立场