一 完全平方数
平方数是指能够表示成某整数平方的数,亦可称为完全平方数.
二 平方数的基本性质:
(1)平方数末位数只能是0.1.4,5,6,9.也可以说是,末位为2,3,7,8的数一定不是平方数;
(2)偶数的平方是4的倍数,即偶数的平方必是4的倍数;
(3)奇数的平方是4或8的倍数加1,即奇数的平方被4(或8)除余1;
(4)相邻两数之积不是平方数;
(5)平方数与平方数之积必为平方数,平方数与非平方数之积必为非平方数;
(6)平方数若是奇数,则它的十位数字必是偶数;
(7)平方数的所有非负约数的个数是奇数,反之亦真.
(8)从1开始的连续奇数的和等于奇数个数的自乘积。即奇数个数“数的平方”。
(9)1+2+3+4+5+6+7+8+9+10+9+8+7+6+5+4+3+2+1=10×10,即等号左边这样的一串数之和等于中间数的自乘积。中间数的平方。
1+2+3+4+…(n-1)+n+(n-1)+…+4+3+2+1是一个平方数(中间数n的平方)
三 实例分析
分析 1=1×1
1+2+1=2×2
1+2+3+2+1=3×3
1+2+3+4+3+2+1=4×4
1+2+3+4+5+4+3+2+1=5×5
1+2+3+4+5+6+5+4+3+2+1=6×6
......
1+2+3+4+…(n-1)+n+(n-1)+…+4+3+2+1=n×n
则当n=100时1+2+3+4+…+98+99+100+99+98+…+4+3+2+1=100×100
=10000
【实例2】【求和1+3+5+7+9+11+13+15+17+19=————
分析
1+3+5=3×3
1+3+5+7=4×4
1+3+5+7+9=5×5
1+3+5+7+9+11=6×6
1+3+5+7+9+11+13=7×7
1+3+5+7+9+11+13+15=8×8
1+3+5+7+9+11+13+15+17=9×9
1+3+5+7+9+11+13+15+17+19=10×10
则
1+3+5+7+9+11+13+15+17+19=100

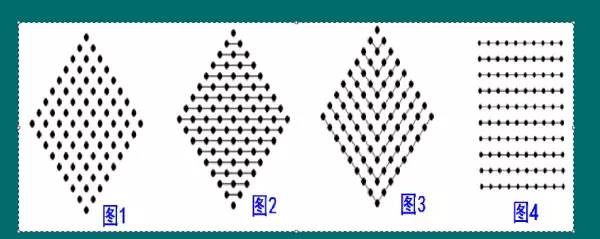
数一数图1中有多少个点?

三种求解方法---结果是完全平方数
【实例3】一个自然数减去45及加上44都仍是完全平方数,求此数。解:设此自然数为x,依题意可得x-45=m^2................x+44=n^2................-可得n^2-m^2=89, =89但89为质数,它的正因子只能是1与89,于是。解之,得n=45。代入得。故所求的自然数是1981。
【实例4】有一个自然数,减去5是完全平方数,减去61还是完全平方数,请问这个自然数可能是多少?
分析:假设这个自然数是a。
且a-5=m^2。
a-61=n^2。
(其中m^2表示m的平方)。
接着就是寻找它们之间的关系。
步骤1:
先思考第一个问题。
m和n有什么关系?
上面的两个等式相减有:
61-5= m^2-n^2。
化简即56=(m+n)*(m-n)。
步骤2:
再思考第二个问题。
m和n是多少?
首先m+n与m-n一定同奇同偶。
在56的分解中。
只有2*28,4*14是同奇同偶的。
因此答案共有两种情况:
第一种是m-n=2,m+n=28。
此时m=15,n=13;
第二种是m-n=4,m+n=14。
此时m=9,n=5。
步骤3:
综合上述两个问题。
在步骤2的基础上分情况讨论:
当m=15,n=13时,a=m^2+5=230;
当m=9,n=5时,a=m^2+5=86。
所以这个自然数可能是230或86。