组合数是指从 n 个不同元素中,任取 m 个元素并成一组,叫作从 n 个不同元素中取出 m 个元素的一个组合;从 n 个不同元素中取出 m 个元素的所有组合的个数,叫作 n 个不同元素中取出 m 个元素的组合数1。用符号 C 表示。
例如,从 {a,b,c,d} 中任取两个元素,可以得到六种组合:{a,b}、{a,c}、{a,d}、{b,c}、{b,d}、{c,d}。所以 C = 6。
那么如何计算 C 呢?有以下几种方法:
- 利用公式法
根据排列数和组合数之间的关系,可以得到以下公式1:
C = A / m! = n! /
其中 A 表示从 n 个不同元素中取出 m 个元素的排列数,n! 表示 n 的阶乘,m! 表示 m 的阶乘。
例如,C = A / 2! = / = 12 / = 6
这种方法比较简单直接,但是当 n 和 m 很大时,阶乘运算会很复杂。
- 利用递推法
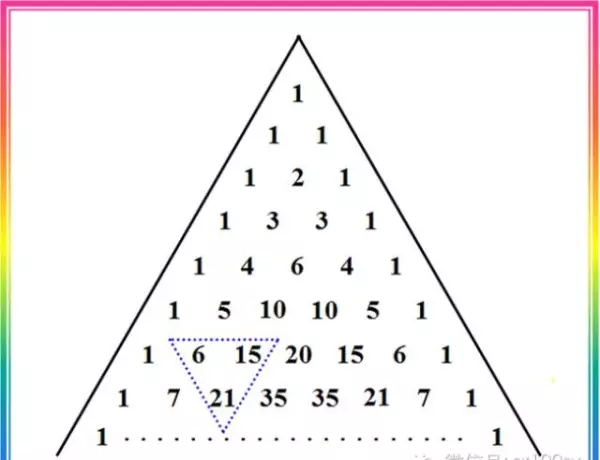
根据杨辉三角形(帕斯卡三角形)的性质4,可以得到以下递推公式:
C = C + C
其中 C(n,0)=C(n,n)=1
例如。
C=1 C=C=1 C=C=1 C=C+C=2 … 以此类推
这种方法可以避免阶乘运算,但是需要存储前面计算过的结果。
